Selbstähnlichkeit – Die Struktur der Fraktale und die Fibonacci-Spiralen

de.wikipedia.org

Selbstähnlichkeit am Beispiel des Sierpinski-Dreiecks

Selbstähnlichkeit im engeren Sinne ist die Eigenschaft von Gegenständen, Körpern, Mengen odergeometrischen Objekten, in größeren Maßstäben, d. h. bei Vergrößerung, dieselben oder ähnliche Strukturen aufzuweisen wie im Anfangszustand. Diese Eigenschaft wird unter anderem von der fraktalen Geometrie untersucht, da fraktale Objekte eine hohe bzw. perfekte Selbstähnlichkeit aufweisen. Die Mandelbrot-Menge ist streng genommen und im Gegensatz zu häufig zu lesenden Meinungen nicht selbstähnlich: Im Prinzip kann man jedem Ausschnitt des Randes in jeder Vergrößerung bei genügender Auflösung ansehen, von welchem Punkt er stammt.

Im weiteren Sinne wird der Begriff auch in der Philosophie sowie den Sozial- und Naturwissenschaftenverwendet, um grundsätzlich wiederkehrende, in sich selbst verschachtelte Strukturen zu bezeichnen.

Blütenstand des Romanesco mit fraktalen Strukturen und Fibonacci-Spiralen.

Der Teil als Ganzes

Andreas Walker | Ausgabe 3 – 2008

Selbstähnlichkeit ist eine häufige Erscheinung in der Natur. Ob bei Farnen oder Küsten – die Struktur des Ganzen zeigt sich oft auch in seinen Teilen.

Unser Planet ist Bestandteil einer Planetenfamilie mit der Sonne als ihrem Muttergestirn im Zentrum. Unsere Sonne und unser Sonnensystem ihrerseits sind wiederum Bestandteil der Milchstrasse, einer Galaxie, die aus rund 200 Milliarden Sonnen besteht. Die Milchstrasse ist Mitglied in einem sogenannten Galaxienhaufen und die Experten gehen davon aus, dass diese Galaxienhaufen erneut in Haufen zusammengelagert sind. Neueste Erkenntnisse in der Kosmosforschung lassen vermuten, dass sogar unser Universum nur ein Teil eines noch grösseren Universums ist – eine einzelne Seifenblase in einem Konglomerat von vielen Seifenblasen, wie es der russische Kosmologe Andrei Linde formuliert.

Makrokosmos und Mikrokosmos

Solche Phänomene, bei denen sich die ursprüngliche Struktur eines ganzen
Objekts auch in ihren immer kleiner werdenden Teilen wiederholt, werden in den Naturwissenschaften als Selbstähnlichkeit bezeichnet. Selbstähnliche Muster treten nicht nur in makrokosmischen Grössenordnungen auf, sondern finden sich auch im Kleinen und Kleinsten der Materie. Diese erweist sich als Verbund von Molekülen und Atomen. Die Moleküle setzen sich aus verschiedenen Atomen zusammen. Die Atome, lange als Grundbausteine der Materie betrachtet, bestehen aus Neutronen, Protonen und Elektronen. Neutronen und Protonen bilden die Atomkerne und sind wiederum aus verschiedenen sogenannten Quarks zusammengesetzt.

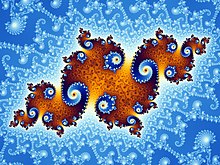
Von exakter Selbstähnlichkeit ist die Rede, wenn die Repetition der Gesamtstruktur eines Objekts in dessen Teilen bis zur Unendlichkeit bestehen bleibt. Dies ist nur bei Objekten der Fall, die mit Hilfe mathematischer Algorithmen künstlich erzeugt werden. Ein berühmtes Beispiel ist eine als Mandelbrotmenge oder Apfel- männchen bezeichnete geometrische Struktur (siehe Abbildung). Der französische Mathematiker Benoît Mandelbrot, auf den diese zurückgeht, erkannte in den 60er-Jahren die Selbstähnlichkeit natürlicher und künstlicher Gebilde und prägte dafür den Begriff Fraktal. Dieser leitet sich vom Lateinischen «fractus» (gebrochen) oder «fragere» (in Stücke brechen) ab.

Durch eine mathematische Formel generierte Mandelbrot eine Zahlenmenge und stellte diese grafisch dar. Es entstand ein perfektes fraktales Gebilde, dessen geometrische Formen sich auf allen Grössenstufen wiederholten. Aufgrund der hohen Ästhetik fraktaler Bilder begann sich in der Folge auch ein Teil der Kunstszene für Fraktalgeometrie zu interessieren. In Computersimulationen wird diese zudem zur Schaffung realitätsnaher Landschaften eingesetzt. Ebenfalls lassen sich mit ihr Verläufe chemischer Reaktionen, das Wachstum von Kristallen oder das Verhalten von Flüssigkeitsmischungen simulieren und verstehen.

Repetition im Pflanzenblatt

Mandelbrot war überzeugt, dass die geometrische Struktur vieler natürlicher Erscheinungen wie Gebirge, Wolken oder Sternhaufen ebenfalls auf dem Prinzip der Selbstähnlichkeit beruhen oder Fraktalen zumindest ähnlich sind. Tatsächlich weisen viele in der Natur vorkommende Strukturen eine solche Tendenz auf. Verschiedene Küstenverläufe beispielsweise zeigen bei unterschiedlich gross gewählten Ausschnitten Selbstähnlichkeit: Ob man einen ganzen Küstenstreifen betrachtet, auf einen bestimmten Abschnitt oder auf eine einzelne Bucht zoomt, es zeigen sich ähnliche geometrische Muster.

Auch wer einen Farn betrachtet, erkennt oftmals das Prinzip der Selbstähnlichkeit. Der Bauplan der Pflanze wiederholt sich über teilweise mehrere Verästelungsstufen – vom ganzen Wedel über die Teilblätter bis zu den Fiederchen. Hier zeigt sich auch deutlich, dass sich im Gegensatz zum mathematischen Fraktal die Selbstähnlichkeit in der Natur meist nur über wenige Stufen fortsetzt. Ein eindrückliches Beispiel von Selbstähnlichkeit tritt beim Romanesco auf. Die Gesamtform dieser Kohlsorte wiederholt sich in der gleichen Art und Weise in immer kleineren Einheiten. Fokussiert man seinen Blick auf ein einzelnes Röschen, erblickt man wieder die Gesamtform des Romanescokopfes. Auch dessen naher Verwandter, der Blumenkohl, zeigt einen fraktalen Aufbau.

Deutlich sichtbar ist das Prinzip der Selbstähnlichkeit zudem bei vielen Bäumen und ihren Blättern. Ein frei stehender Baum, der von allen Seiten genügend Licht erhält und nicht geschnitten wird, weist in der Regel eine ähnliche Form auf wie seine Blätter, wobei die Verzweigungs- muster der Äste Ähnlichkeiten mit jenen der Blattnerven aufweisen können. Betrachtet man im Winter den blattlosen Baum, so erscheint seine gesamte Silhouette oftmals wie ein einzelnes Blatt. Die Grundform des ganzen Baumes findet sich häufig auch in seinen einzelnen Teilbereichen wieder. Die Selbstähnlichkeit macht auch vor dem Menschen nicht Halt. Wie die Blattadern oder wie Flusssysteme verästeln sich Blutgefässe oder Nervenfasern ebenfalls in fraktaler Manier.

Spiralen und Wirbelstürme

Eine andere Art von Selbstähnlichkeit offenbart sich in der universellen Form
der Spirale. Wirbelförmige Gebilde sind überall in der Natur anzutreffen: Kleine Wasserwirbel in einem Fluss, die sich hinter einem Brückenpfeiler bilden, liegen im Zentimeterbereich; ein Tiefdruckgebiet kann einen Durchmesser von 1000 Kilometer einnehmen und eine Spiralgalaxie kann ohne Weiteres 100 000 Lichtjahre gross sein. Ein Lichtjahr entspricht einer Distanz von rund 9,5 Billionen Kilometern. Unabhängig von der Grössenordnung manifestiert sich die Spiralstruktur als universelles Prinzip.

Ein vergleichbares Beispiel von Ähnlichkeit aus der Meteorologie sind Thermik- schläuche, die in verschieden- sten Grössen in Gasen entstehen. Betrachtet man zum Beispiel eine Tasse heissen Kaffees, so kann man hin und wieder kleine rotierende Dampfsäulen ausmachen, die über der Flüssigkeit aufsteigen – Mini-Tornados im Zentimeterbereich. Dasselbe Prinzip erscheint in viel grösserer Erscheinung in einem echten Tornado, der bei einem Kälteeinbruch über stark aufgewärmtem Land entsteht. Der Durchmesser eines Tornados kann einen Durchmesser von einigen bis zu 500 Metern oder noch mehr betragen.

Bei der Betrachtung von Selbstähnlichkeit oder vergleichbaren Phänomenen in der Natur wird offensichtlich, dass trotz ganz unterschiedlicher Dimensionen und Grössenordnungen hinter der scheinbar grenzenlosen Vielfalt an Formen Grundstrukturen existieren, die in jedem Massstab sichtbar werden: im Grössten wie im Kleinsten.

Bilder: René Berner natuerlich-online.ch

Bildquelle: hoetzel.wordpress.com

Dazu auch der Videovortrag von Andreas Beutel:

Geometrie, Raum Zeit und Bewusstsein – Andreas Beutel (Pythagoras Institut)

In diesem Vortrag werden einzelne Erkenntnissen aus Quantenphysik und Bewußtseinsforschung einen möglichen Wirkmechanismus zum Austausch von Bewußtsein und Information zugeordnet.

Vortrag von Andreas Beutel anlässlich des Quantica Kongresses „Evolution – Bewusstsein – Quantenphysik“ vom 14./15. Mai 2011.

Weitere Informationen unter http://www.Quantica.TV

Für viele weitere Filme, Dokus und Reportagen besuche unseren Kanal: https://www.youtube.com/user/NuoVisoTv

Abo: http://www.youtube.com/subscription_c…